Decision tree
Zhengyang Fang
June 21, 2019
Last updated: 2019-08-28
Checks: 7 0
Knit directory: stats-topics/
This reproducible R Markdown analysis was created with workflowr (version 1.4.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20190616) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: analysis/.RData
Ignored: analysis/.Rhistory
Unstaged changes:
Deleted: .gitlab-ci.yml
Deleted: public/.nojekyll
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the R Markdown and HTML files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view them.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| html | 12621f3 | Zhengyang Fang | 2019-06-21 | decision tree |
| Rmd | 8c0a05e | Zhengyang Fang | 2019-06-21 | wflow_publish(“decision_tree.Rmd”) |
| html | 37e0ede | Zhengyang Fang | 2019-06-21 | update .docs |
| Rmd | 91c33bb | Zhengyang Fang | 2019-06-21 | wflow_publish(“decision_tree.Rmd”) |
Decision tree
A decision tree displays an algorithm that only contains conditional control statements.
Building the decision tree
We use a divide-and-conquer algorithm to build a decision tree: we split a big node into a few sub-nodes, and then keep splitting those sub-nodes as above, until each of them contains only one class.
In splitting, the rule of thumb is, we split the big node in a way that maximizes the “purity” of those sub-nodes. That is to say, each sub-node contains more samples from only one class.
Information entropy is a measurement of the “purity” of a set. Assume a set \(D\) contains \(N\) classes, and their proportions are \(p_1,p_2,\dots,p_N\). The definition of information entropy is \[
H(D)=-\sum_{k=1}^Np_k\log p_k.
\] The smaller \(H(D)\) is, the higher purity that set \(D\) has.
ID3algorithm (Quinlan, 1986)
Among all possible splitting, choose the attribute \(a\) that maximizes the information gain: \[
Gain(D,a)=H(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}H(D^v),
\]
where \(V\) is the number of possible values of attribute \(a\).
It makes some sense, however, it is in favor of the attribute that splits the node into more sub-nodes. Specifically, if we include the idendity attribute in our feature, i.e. each sample has a unique indentity, then it will increase the information entropy to zero. Thus the indentity will always be the chosen one to split. But the generalization ability of this decision tree will be poor, which is not plausible.
C4.5algorithm (Quinlan, 1993)
To avoid splitting the node into fragiles,C4.5 algorithm takes the number of sub-nodes into account. It maximizes gain ratio instead of information gain. The definition of gain ratio: \[
GainRatio(D,a)=\frac{Gain(D,a)}{IV(a)},
\] where \(IV(a)\) is the intrinsic value of attribute \(a\), defined by \[
IV(a)=-\sum_{v=1}^V\frac{|D^v|}{|D|}\log \frac{|D^v|}{|D|}.
\]
A notable fact is that, by maximizing the gain ratio, it tends to choose attributes with less sub-nodes, exactly the opposite to ID3 algorithm. \(C4.5\) algorithm takes both of them into account: it maximizes the gain ratio only among those attributes with information gain above the average.
CART(classification and regression trees, Breiman et al., 1984)
CART uses a new measurement of “purity”: Gini index, defined as follows: \[
Gini(D)=\sum_{k=1}^N\sum_{k^\prime\neq k}p_kp_k^\prime=1-\sum_{k=1}^Np_k^2.
\] The notation is the same as above. For any attribute \(a\), splitting by \(a\) changes the Gini index to \[
Gini(D,a)=\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v).
\]
CART maximizes \(Gini(D,a)\) among all possible attributes \(a\).
Pruning
To prevent overfitting, we prune the decision tree for a better generalization performance.
Prepruning
When building the decision tree, we may stop early, not necessarily until each node contains only one class. For each splitting, we use cross-validation to test whether the current splitting increases the generalization performance. If not, we stop splitting the current node immediately.
Prepruning can reduce the fitting complexity, but it risks ill-fitting. Some splittings themselves cannot improve generalization performance, but based on those, some further splittings may be very helpful. But prepruning totally ignores them.
Postpruning
After we expand all the nodes of a decision tree, we can prune it from the leaf nodes to the root. We also use cross-validation to test whether the current splitting increases the generalization performance. In the comparison, we can take the “good future splitting” into account. Therefore, compared with prepruning, it is much less likely to get ill-fitted. However, since we have to expand all possible nodes at first, and then test all of them, the computation can be a burden.
Other issues
Continuous variable
Continuous variable is more complicated here, because it may have infinite possible values. An easy solution is to sort all the training data by this variable \(a\), suppose their values are \(a_1<a_2<\dots<a_n\), and then treat it as \((n-1)\) possible bi-partition attributes: “whether \(a>T_i?\)”, where \(T_i=\frac12(a_i+a_{i+1}),1\leq i\leq n-1\).
Missing value
Missing value on some attributes is a common issue, especially on clinical data set. Based on \(C4.5\) algorithm, we expand the definition of information gain to solve this issue. The motivation here is, when we split a node with an attribute \(a\), for those samples with missing value on \(a\), we let them appear in all sub-nodes, but with an estimated probability.
For set \(D\), attribute \(a\), let \(\tilde D\in D\) denotes the subset of \(D\) where attribute \(a\) is not missing. We assign a weight \(w_x\) to each sample \(x\), initially \(w_x=1\) for all \(x\).
Define the non-missing proportion \[
\rho=\frac{\sum_{x\in \tilde D} w_x}{\sum_{x\in D}w_x},
\] the proportion for the k-th class in the non-missing data \[
\tilde p_k=\frac{\sum_{x\in \tilde D_k} w_x}{\sum_{x\in \tilde D}w_x},
\] the proportion for taking value \(a^v\) on attribute \(a\) \[
\tilde r_v=\frac{\sum_{x\in \tilde D^v} w_x}{\sum_{x\in \tilde D}w_x}.
\] Then the definition of information gain is generalized as \[
Gain(D,a)=\rho\left(H(\tilde D)-\sum_{v=1}^V\tilde r_vH(\tilde D^v)\right),
\] where \(H(\tilde D)=-\sum_{k=1}^N\tilde p_k\log \tilde p_k\).
For those samples with non-missing value on attribute \(a\), we devide them into the corresponding nodes, and remain their weight \(w_x\) constant. For those samples with missing value on attribute \(a\), we devide them into all possible nodes, but setting their weights to be \(\tilde r_vw_x\). This weight is exactly the estimated probability.
Example
R-package for CART algorithm.
library(rpart)
library(rpart.plot)
library(tree)
data(kyphosis)
set.seed(1)
tree <- rpart(Kyphosis ~ . , kyphosis)
rpart.plot(tree)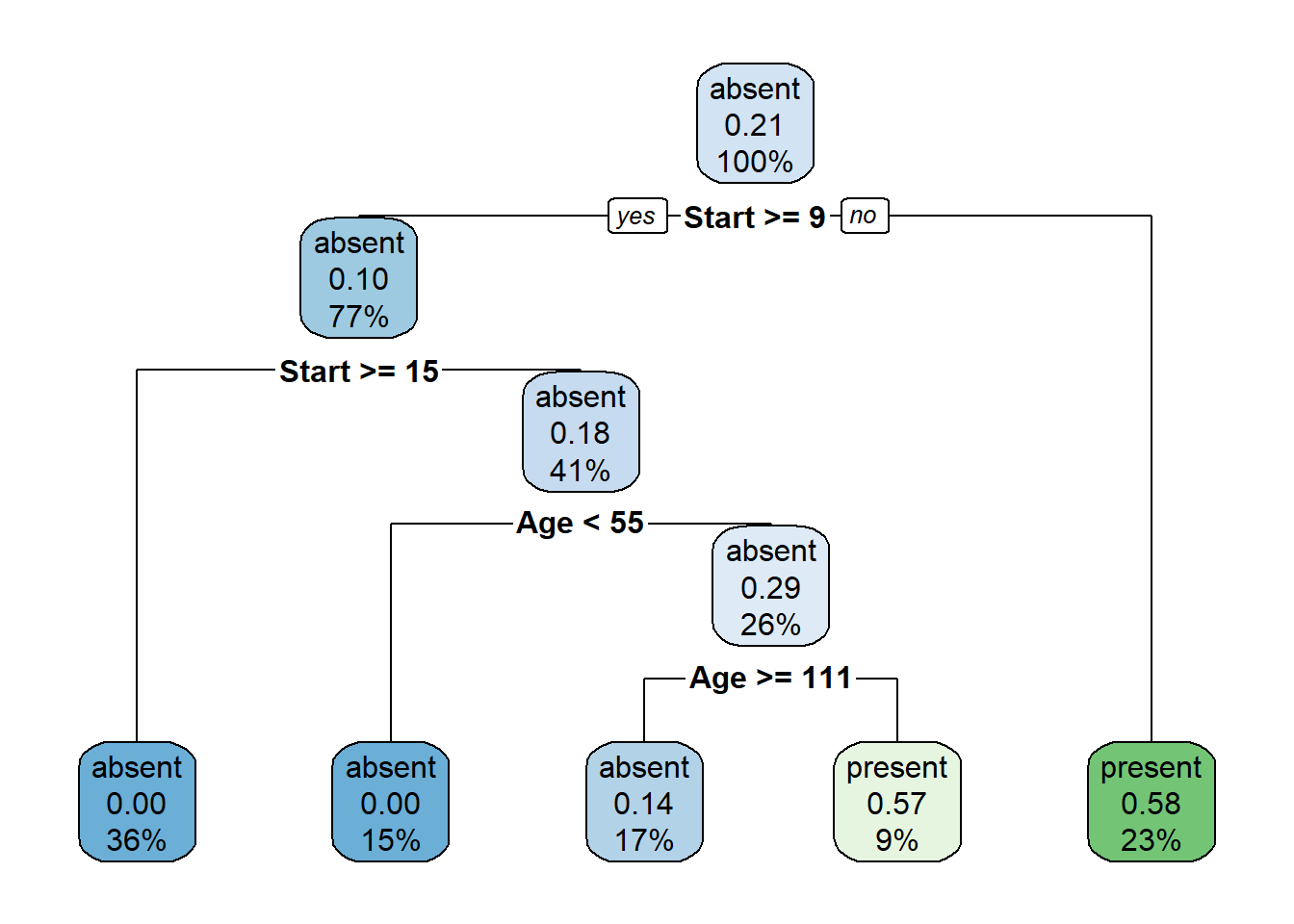
| Version | Author | Date |
|---|---|---|
| 7b6b016 | Zhengyang Fang | 2019-06-21 |
sessionInfo()R version 3.6.0 (2019-04-26)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 17134)
Matrix products: default
locale:
[1] LC_COLLATE=English_United States.1252
[2] LC_CTYPE=English_United States.1252
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C
[5] LC_TIME=English_United States.1252
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] tree_1.0-40 rpart.plot_3.0.7 rpart_4.1-15
loaded via a namespace (and not attached):
[1] workflowr_1.4.0 Rcpp_1.0.1 digest_0.6.19 rprojroot_1.3-2
[5] backports_1.1.4 git2r_0.25.2 magrittr_1.5 evaluate_0.14
[9] stringi_1.4.3 fs_1.3.1 whisker_0.3-2 rmarkdown_1.13
[13] tools_3.6.0 stringr_1.4.0 glue_1.3.1 xfun_0.7
[17] yaml_2.2.0 compiler_3.6.0 htmltools_0.3.6 knitr_1.23